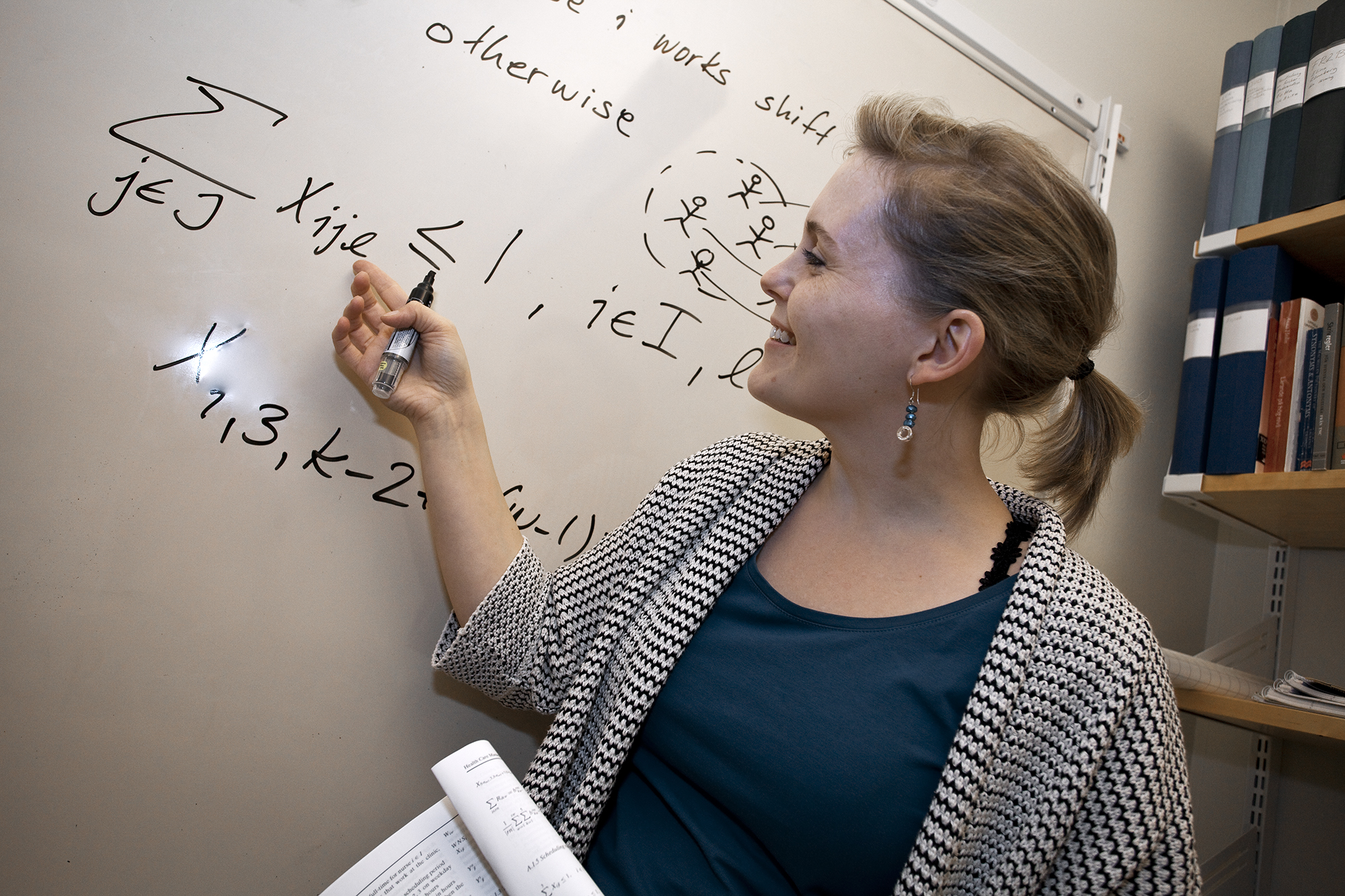Fundamental mathematical research covers widely different parts of mathematics, such as algebra, geometry, graph theory, combinatorics, topology, and several fields of analysis such as differential equations, dynamic systems, function spaces and potential theory.
These fields of mathematics are applied throughout the whole of science, within the natural sciences, medicine, economics and technology. Our focus in fundamental research, however, is often on fundamental scientific questions, with the aim of deepening understanding and developing modern mathematics. The deeper understanding contributes subsequently to many future applications, some of them whose nature is today completely unknown.
Optimisation treats complex decision-making systems with many variables, which makes them difficult to solve. New algorithms and mathematical models are required for truly intractable problems. Applications are found within everything from scheduling and the optimisation of snow ploughing, to planning electrically operated public transport and placing unmanned flying vehicles in communication networks.
Mathematical statistics deals with, for example, multivariate normal distributions in which a model for the expected value (the mean value if an experiment is carried out an infinite number of times) is available, together with a matrix of values that varies in a predictable manner. The methods developed can be applied in many areas in biology, medicine, sociology, technology and economics.
The theory of random number matrices is another field studied. Random number matrices can be used as tools in fields such as financial mathematics, theoretical physics and wireless communication.
Within computational mathematics LiU researchers work with, among other things, time-dependent partial differential equations. These are highly significant in, for example, the simulation of turbulence around aircraft and in simulations in which certain initial conditions are poorly known. One example of application is the design of aircraft, where it is necessary to deliver a simulation with a given, very small margin of error.
Mathematics research is also carried out within areas such as how to use ever-improving methods and models to calculate population growth and magnitude, together with the risk of species extinction and ecological collapse. Researchers are also working to model the human blood stream completely, including the blood vessel walls and the effects of surrounding muscle.
Mathematical teaching theory is a research area in which researchers examine new aids such as tablet computers for teaching maths in special needs schools, and educational methods for children various physical disabilities.